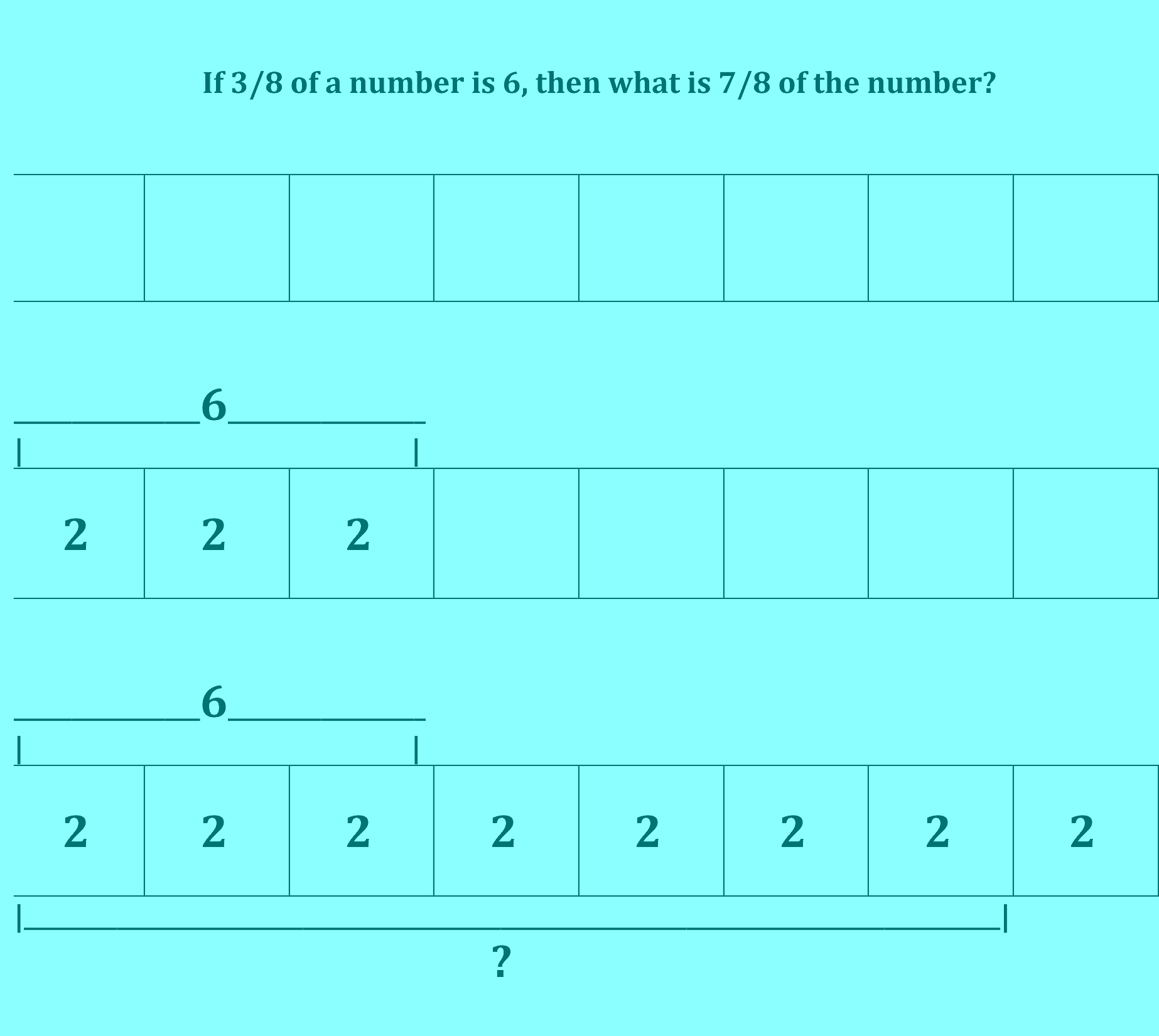
If 3/8 of a number is 6, then what is 7/8 of the number?
A number of years ago*, I was sitting near my daughter who was practicing for the SAT (exam used for admissions to many colleges in the U.S.). Looking over her shoulder, I decided I would use the model drawing method (sometimes called the Singapore Model Method), which I had recently learned, to try to solve some of the problems that she was working on. The way I solved this problem is shown sequentially above (although I only drew the bottom diagram). (My answer was 14, by the way, which would replace the question mark in the diagram.)
In comparison, my daughter used the standard algebraic method with steps something like this:
Step 1: Find the (total) number.
3/8 (n) = 6
n = 6 x 8/3
n = 48/3 (OR perhaps n = 6/1 x 8/3 = 2/1 x 8/1)
n = 16
Step 2: Find 7/8 of the number.
7/ 8 (16) = x (OR perhaps x = 7/8 (16/1) = 7/1 (2/1) )
112/8 = x
14 = x
Both methods:
- Map the information in the problem accurately.
- Allow information to be written down so there is a visible (and verifiable) record.
- Can result in accurate solutions.
However, model drawing allowed me to finish more quickly — not because I was “smarter” but because using model drawing allowed me to work “smarter” (faster and still accurately) because of the way model drawing works*:
- Model drawing can help us to see the big picture, more than sequential steps in which the goal may be lost. (How many times do we see students forget what they are solving for?)
- Fractional parts are graphically shown, so the sizes and relationships of 3/8, 7/8, and the unknown number are easily seen and labeled.
- For this problem (and many others), numbers are more easily handled. (We can start with the 6, which can be easily divided into 2’s. One doesn’t even need to calculate 7/8 of 16 or 112/8.)
Elegant solutions are those in which the desired result is achieved simply, clearly, and without unnecessary complication. In model drawing, problems that seem complicated often are made simple.
Of course, any tool can be misused. Using any tool well requires understanding and discipline.
Lack of understanding and discipline in attending to what is important certainly leads to many errors in algebraic calculations. (Ever see students mistakenly depend on “key words” to decide which calculation they’ll use? Or make calculation errors when they run steps together like 16 + 9 = 25 – 13 = 12/2….?)
So how does model drawing fit into a math curriculum?
In the Singapore math curriculum, model drawing is a basic method introduced to young students in their first years of school. Model drawing becomes a bridge to algebraic mapping of word problems because, despite all of its benefits, the model drawing method has limitations as to the mathematical problems it can address.
However, model drawing is an essential method, a missing piece for curricula that jump too fast to abstract representations and to what are often presented as seemingly arbitrary rules of when and where to move numbers in equations. Model drawing shows visually the structure of problems and helps students to understand the relationships between numbers (and variables). And students may find it fun to try to solve problems, like the one I picked out of an SAT preparation book, more quickly and easily.
*Model drawing has been around for decades. Why post this now?
Although I wrote some about model drawing for myself a few years ago, I was sidetracked by newer interests. I also thought that perhaps there was enough written about model drawing already.
But now it seems that still not enough people know about model drawing.
Model drawing deserves to be well-known. The only way to move past overgeneralizations and opinions with little foundation about better teaching methods is to look at specific examples.
**reminiscent of Don Norman’s book title, Things That Make Us Smart
- My Xyla and Yabu App: Are the Word Problems Too Much? - September 24, 2016
- Model Drawing — An Essential Tool that Makes Us Smarter - September 9, 2016
- To What Should We Have to Pay Attention? - October 2, 2014