In elementary school math, students learn how to change a mixed fraction to an improper fraction. Here is a tip or trick that teachers may use in their instruction:
The visual diagram cues the student to multiply: 5 x 1 = 5.
Then the student adds: 5 + 2 = 7.
This series of steps is highly dependent on the visual diagram for its effectiveness. Without the diagram, we might be forced to use words like these: “Multiply the denominator by the whole number in the mixed fraction. Add the result to the numerator to get the numerator of the improper fraction. The denominator of the improper fraction remains the same.”
Because this explanation may seem rather complicated (and may still lead to errors), occasionally one hears something closer to: “Multiply the bottom number by the big number. Add it to the top number to get the new top number.” As you can see, this trick is often made much worse by the way it is presented.
Does this trick help students to understand the relationship between mixed and improper fractions? What would prove that students understand?
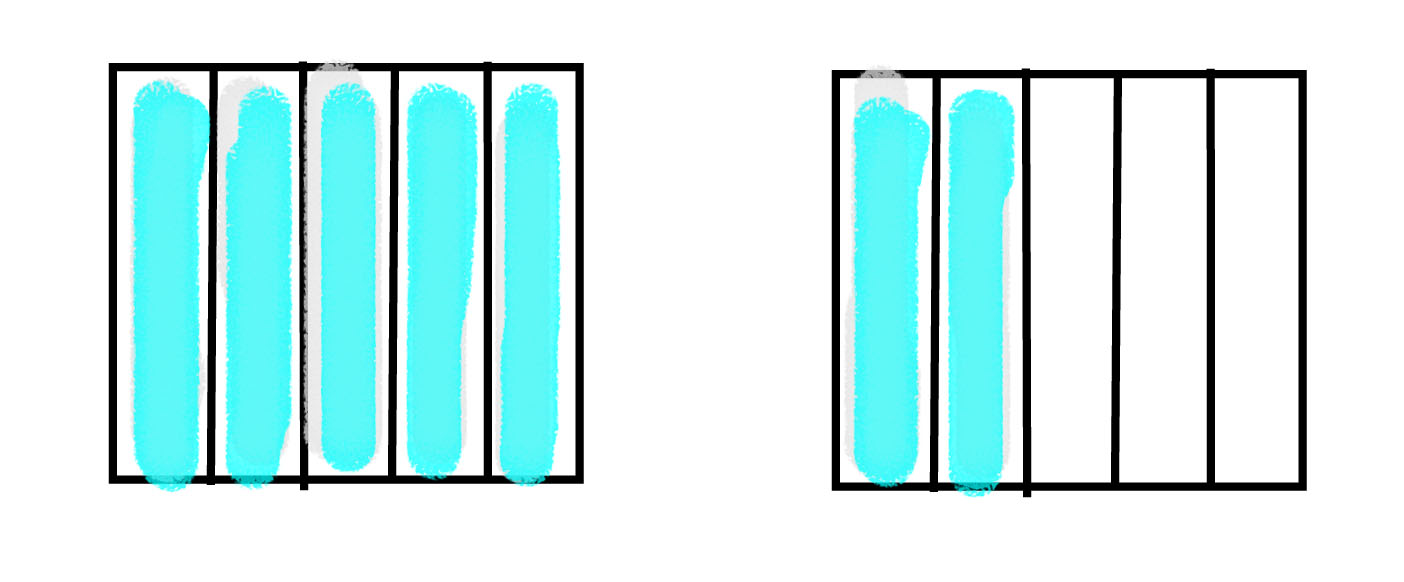
Well, to show understanding, students should be able to show in a drawing of objects that 1 2/5 is the same as 7/5.
Students also should be able to show that 1 2/5 is the same as 7/5 on a number line.
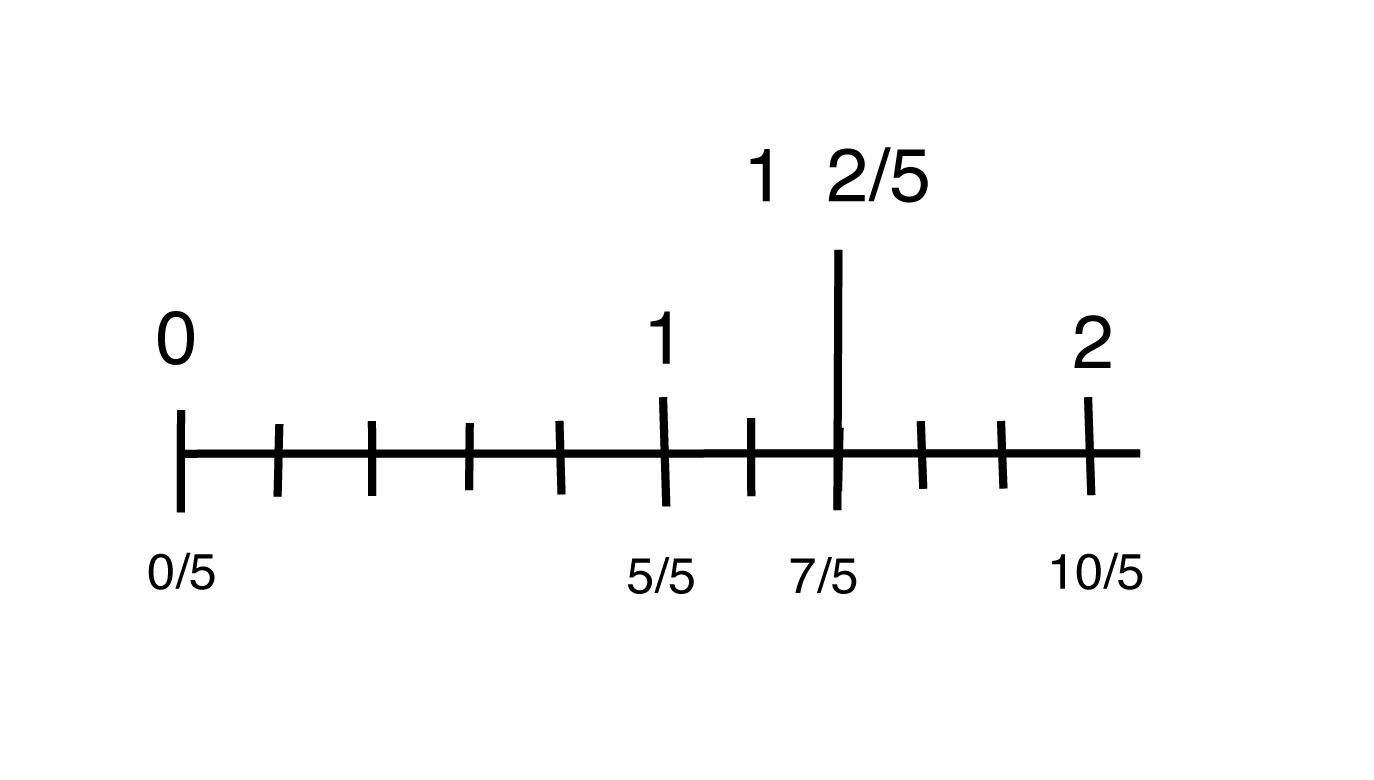If they cannot prove their results in these ways, students do not really understand what they are doing.
If students don’t understand why they are following what may seem to be arbitrary steps of this trick, they are only mimicking a machine. They are possibly mimicking a faulty machine, as well, because students are likely as time goes on to forget the details of this visual trick. They may forget where to put the x and the + signs and what to do with them.
In comparison, the following is a better mapping of what mixed and improper fractions represent:
This better mapping depends on prior accurate understanding. Students must know fractions that equal 1 (and other whole numbers, as they work with other mixed numbers). They must also understand how to add fractions. If students do not really understand these basics, teachers and students may need to depend on superficially helpful tips and tricks that at least allow them to pass the next test.
Whenever we encounter a tip or a trick, we must evaluate whether it furthers children’s understanding. In the long run, if tips and tricks are not based on meaningful understanding, students are unlikely to have the foundations for future learning.
- My Xyla and Yabu App: Are the Word Problems Too Much? - September 24, 2016
- Model Drawing — An Essential Tool that Makes Us Smarter - September 9, 2016
- To What Should We Have to Pay Attention? - October 2, 2014