Merrie, a fourth grader, is confronted with the following question:
If Henry ate 1/3 of 3 pizzas, how much did he eat?
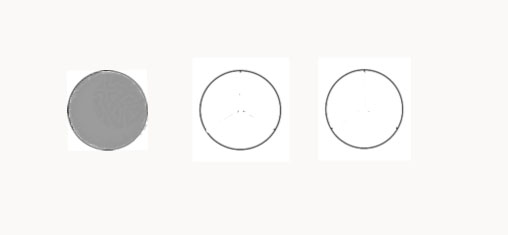
Merrie draws this picture to help her solve the problem:
Merrie’s drawing shows 3 pizzas divided into thirds. She shades 1/3 of 1 of the pizzas. Why does Merrie think of the problem in this way?
From Merrie’s drawing, it seems quite likely that she knows one, very simple version of one way of thinking about fractions. (She also may be depending on her common sense belief that Henry shouldn’t be eating more than 1/3 of a pizza!)
Many children get stuck in one way of thinking. Dividing one whole, often a pie or a pizza, is an early, common example and picture. Students who make Merrie’s error usually assume that all fractions are the same. In fact, there are many ways to interpret numbers with numerators and denominators. For instance, fractions can represent division, ratios, rates, slopes of lines, and points on a number line.
In early grade school, students work primarily with problems that use two ways of thinking about fractions: a fraction of a whole and a fraction of a set or group of items. Sometimes the difference is never addressed directly.
The fraction of a whole model divides an area into equal parts. The fraction of a group model divides items into equal subsets of items.
Fraction of a whole model
Perhaps students who understand the fraction of a whole model well would not make Merrie’s mistake. They might think of 1/3 of the whole area of three pizzas.
Or they might shade 1/3 of each pizza and end up with 3/3 or 1 pizza.
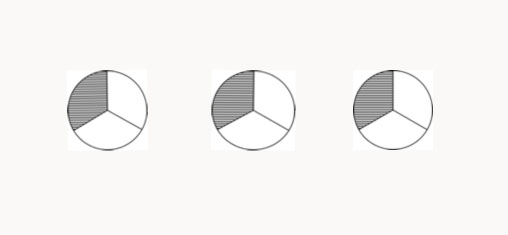However, they might think the problem too unwieldy if they were asked about 1/3 of 24 pizzas, or horrors, 2/3 of 24 pizzas.
Fraction of a group model
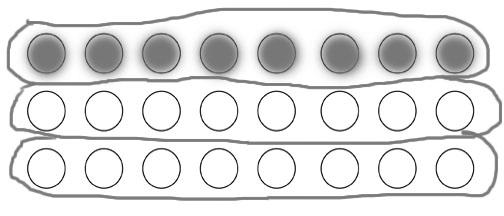
Students who understand the fraction of a group model would know that 1/3 of 3 pizzas — when three pizzas are separated into three different equal groups — is one pizza. They could use a similar procedure to divide 24 pizzas into 3 groups to figure out that 1/3 of 24 pizzas is 8 pizzas (the number of pizzas in one of the 3 equal groups).
They also could see that 2/3 of 24 pizzas is 16 (the number in two of the 3 equal groups)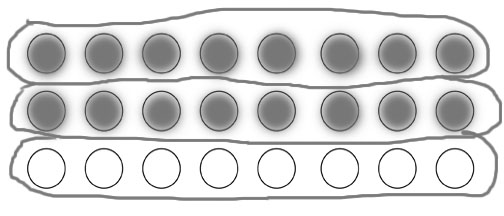 
As the difficulty of problems increases, if children do not understand the difference between the underlying structure of the two models, they will probably become more confused. Without clear and deep understanding, mistakes may occur even among students who passed weekly tests on one kind of problem or the other. Students may use the wrong models of fractions when they meet them again a month or a year later.
Lessons That May Confuse Instead of Clarify
Not all lessons clear up the confusion. The following text and illustrations are from an older 4th grade math textbook.** See if you as an adult reader can easily discriminate how the two different models of fractions are used. Then try to view these ideas from a child’s vantage point.
Do you see where the fraction of a whole (area) model is used?
The garden, which is meant to be an example of the whole model includes objects (different numbers of pea, tomato, and cabbage plants), so it is not a simple and clear illustration of only the area model. (One could conceivably make up word problems using the set of items model with the objects in the garden plot.) Furthermore, although the 3 thirds of the garden by definition are equal parts, am I the only reader subject to an optical illusion that the three sections of the garden are not the same size?
Do you see where the fraction of a set of items model is used?
The example of the peapods is also potentially confusing. The units in the set of items are peapods, but the peas in several of the peapods are another, potentially confusing level of units. For the purposes of the description in the text, the number of peas in the peapods is not important but the number of peapods with peas in them is. (Got that?) The number of peapods with onions (none) in them is also important.
The way I’m describing these pictures is confusing, of course. If no one says anything more than what is in the text, teachers and students might believe that the ideas are clear and understandable — to someone — if not to themselves. The words and pictures do appear with clarity on the page! However, what students remember and can apply independently afterwards may be confused and inaccurate.
For whom and how many does math education “work”?
Some people may still wonder why they should care about models of fractions and whether and how they are presented to students. “But it works!”
Much of current U.S. math education works well for a subset of students, but fewer and fewer go on at each grade to understand math with enjoyment and confidence. We need to look at the specifics of what and how we teach and how well children learn what we’re teaching. Only by observing the nitty-gritty details can we design better lessons for everybody.
* We could find more reasons, but this is a start!
** I’ve found similar garden pictures and descriptions in many other textbooks, including recently published ones. Sometimes the presentation is better, but how much “better” is enough? What kinds of illustrations and examples would help all students to understand more quickly and easily?
The garden illustration can be used for discussions and as a rich source of questions. However, students who need clear information may be left confused if this illustration and description are what they’re depending on for instruction.
- My Xyla and Yabu App: Are the Word Problems Too Much? - September 24, 2016
- Model Drawing — An Essential Tool that Makes Us Smarter - September 9, 2016
- To What Should We Have to Pay Attention? - October 2, 2014